쉽게 설명하는 알고리즘 시리즈, 대망의 1편입니다.
계속 연재할지 중간에 슬쩍 사라질지는 저도 모르겠지만, 아무튼 열심히 해 보겠습니다.
다양한 알고리즘들을 직접 공부하고, 하나씩 소개하는 방식으로 진행됩니다.
첫 번째 알고리즘은, Z 알고리즘입니다.
Z 알고리즘이란?
 Z Array
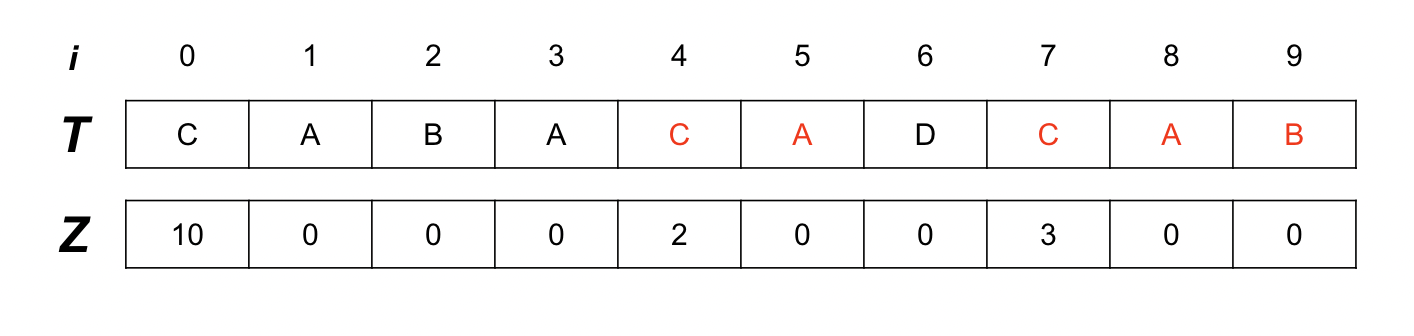
Z Array
Z 알고리즘이란 문자열에서 특정 패턴을 찾는 패턴 검색 알고리즘입니다. O(M + N)의 선형 시간 복잡도를 가집니다.
또한 Z 알고리즘은 현재 인덱스, 즉 String[i]에서 시작하는 가장 긴 접두사 부분 문자열의 길이를 저장하는 배열인 *Z 배열이라는 보조 배열과 함께 작동합니다.
- 접두사 부분 문자열: 문자열의 첫 부분과 일치하는 현재 인덱스부터 시작하는 부분 문자열
Index 0 1 2 3 4 5 6
Text a a b c a a b
Z values N 1 0 0 3 1 0
예를 들어, “aabcaab”라는 문자열에서, 5번째 a의 가장 긴 접두사 부분 문자열은 aab입니다. aabcaab가 시작 부분과 일치하기 때문입니다.
그렇기 때문에 만약 Z[i] = k라면, String[i .. i + k] = String[0 .. k]가 성립합니다. Z 알고리즘은 이 원리를 이용해 선형 시간으로 패턴을 탐색합니다.
쉽게 생각하자면, 패턴과 텍스트를 연결하여 “P$T” 문자열을 생성한다고 생각하면 됩니다. 여기서 P와 T는 접두사, $는 접두사에 포함되지 않는 문자입니다.
만약 Z 배열에서 Z[i]가 임의의 지점에서 접두사 길이와 같으면, 위의 원리에 따라 해당 지점은 접두사 부분 문자열이 존재한다고 볼 수 있습니다.
개념은 이 정도로 하고, 실제 코드를 보며 이해해 봅시다.
구현
fun getZArray(s: String): IntArray {
val n = s.length
// 문자열 크기의 Z 배열을 사용합니다.
val zArray = IntArray(n)
// 선형 시간으로 구성하기 위해 두 개의 포인터 Left와 Right로 접두사 부분 문자열의 간격을 나타냅니다.
var left = 0
var right = 0
// 0번째 인덱스는 문자열 전체가 접두사이기 때문에 탐색은 1부터 시작합니다.
for (i in 1 until n) {
// i가 Right 포인터보다 크다면, i는 두 포인터 사이의 간격(즉, 접두사 부분 문자열) 밖에 있습니다.
// 그렇기 때문에 i 이전에 시작하고 i 이후에 끝나는 접두사 부분 문자열이 없습니다. 즉, 현재의 두 포인터 사이의 간격에서 얻을 수 있는 정보가 없습니다.
if (i > right) {
// 현재의 포인터 값들은 쓸모가 없기 때문에, Left와 Right를 i로 초기화합니다.
left = i
right = i
// i만큼의 간격을 유지하며 Left와 Right가 가리키는 값이 다를 때까지 (즉, 더 이상 접두사 부분 문자열이 아닐 때까지) 간격을 확장합니다.
while (right < n && s[right - left] == s[right]) {
right++
}
// Z[i]를 두 포인터 사이의 간격(접두사 부분 문자열의 길이)으로 설정합니다.
zArray[i] = right-- - left
} else {
// i가 Right 포인터보다 작거나 같다면, 여기부터는 두 가지 경우가 있습니다.
val k = i - left
// 만약 k부터 시작하는 접두사 부분 문자열의 길이가 현재 간격보다 짧다면, 확장할 수 있는 최대 간격이 현재 간격보다 짧다는 것을 의미합니다.
// 따라서 i로부터 시작하는 접두사 부분 문자열의 길이는 최대 k이기 때문에 Z[i] = Z[k]로 설정하고, 간격은 동일하게 유지한 채로 다음 반복으로 넘어갑니다.
if (zArray[k] < right - i + 1) {
zArray[i] = zArray[k]
} else {
// 현재 간격보다 크다면, 현재 간격을 더 확장할 수 있다는 것을 의미합니다. 따라서 위의 코드처럼 간격을 확장하고 Z[i]를 설정합니다.
left = i
while (right < n && s[right - left] == s[right]) {
right++
}
zArray[i] = right-- - left
}
}
}
return zArray
}
코드 예제는 GitHub에서 확인하실 수 있습니다.
연습 문제
모든 공통 접두사의 길이의 합을 구하는 문제입니다. Hard 난이도지만 Z 알고리즘으로 매우 쉽게 해결할 수 있습니다.